概要
個別項の二項分布の確率を計算します。
書式
BINOMDIST(x,n,p,cumulative)
引数
有効な引数は次のとおりです。
| 引数 | 説明 |
|---|---|
| x | 試行に成功した回数。整数以外の値を指定すると、小数部分が切り捨てられます。 |
| n | 独立試行の回数。整数以外の値を指定すると、小数部分が切り捨てられます。 |
| p | 1回の試行の成功率(0 から 1) |
| cumulative | 関数の形式を決定する論理値。True に設定すると、累積分布関数を返します。これは、x 回以下の成功が得られる確率を表します。False に設定すると、確率密度関数を返します。これは、x 回の成功が得られる確率を表します。 |
解説
BINOMDIST 関数は、試験または試行の数が決まっている問題において、互いに排他的な2つの結果(「成功」と「失敗」)が生じ、個々の試行が独立しており、さらに、一方の結果が生じる確率が実験中一貫して一定である場合に使用します。たとえば、次に生まれる3人の新生児のうち、2人が男の子である確率を計算する場合に使用できます。
二項確率密度関数は、次のように計算されます。
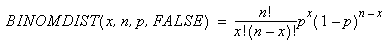
x は成功した回数、n は試行回数、p は1回の試行の成功確率をそれぞれ表します。 累積二項分布は次のように計算されます。
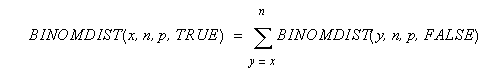
n は試行回数、x は成功した回数、p は1回の試行の成功確率をそれぞれ表します。
データ型
cumulative 引数に対しては論理データを、それ以外の全引数に対しては数値データを受け取り、 数値データを返します。
サンプル
新生児の性別は男か女のいずれかです。ここでは分かりやすいように、その確率を 50/50 と想定します。 女児を True とすると、以下の式によって、次に生まれる 10 人中5人の新生児が女児である確率を算出できます。 最初に産まれる子供が女児である確率は 0.5 であり、10 人の子供のうち厳密に5人が女児である確率は、次のようになります。
BINOMDIST(5,10,0.5,FALSE) 結果:0.2460937500
参照
BETADIST | CRITBINOM | EXPONDIST | GAMMADIST | NEGBINOMDIST | WEIBULL | 統計関数